The goal of CORPlot is to create cumulative odds ratio plot to visually inspect the proportional odds assumption from the proportional odds model. For more explanation on the role of the proportional odds assumption in ordinal outcome analysis, see our paper (Long et. al, 2025).
You can install the development version of CORPlot from GitHub with:
# install.packages("pak")
pak::pak("Yongxi-Long/CORPlot")There are three steps to make a cumulative odds ratio plot, each corresponds to a function in this package:
Users can either directly input to the CORPlot() funtion and this function will do the first two steps internally. Or users can choose to supplied a data frame of odds ratios calculated externally and ask CORPlot to make the plot.
We will use the df_MR_CLEAN example dataset included in the package. It is from a randomized controlled trial investigating endovascular therapy in patients with stroke (Berkhemer et al., 2015). The trial enrolled 500 patients, with 233 assigned to the intervention group and 267 to the control group. The dataset contains three variables:
Because very few patients fell into mRS category 0, we combine categories 0 and 1 into a single category (labeled mRS = 1) to improve representation in the Cumulative Odds Ratio plot.
data("df_MR_CLEAN")
df_MR_CLEAN <- df_MR_CLEAN |>
dplyr::mutate(mRS6 = dplyr::case_when(
mRS <= 1 ~ 1,
TRUE ~ mRS
))res <- CORPlot(
data = df_MR_CLEAN,
formula = mRS6 ~ group,
GroupName = "group",
confLevel = 0.9
)
# show the plot
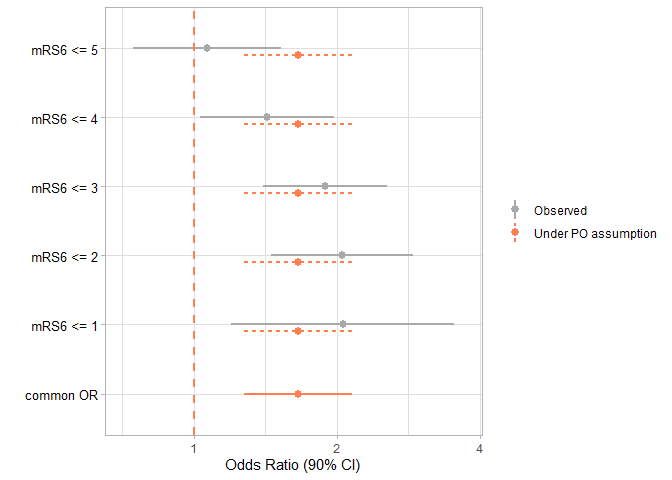
plot(res)
# print the detailed ORs and confidence intervals
print(res,digits = 3)
#>
#>
#> Table: Odds Ratios
#>
#> | Label | OR | lowerCI | upperCI | type |
#> |:---------:|:-----:|:-------:|:-------:|:--------:|
#> | mRS6 <= 1 | 2.056 | 1.196 | 3.534 | Observed |
#> | mRS6 <= 2 | 2.050 | 1.453 | 2.892 | Observed |
#> | mRS6 <= 3 | 1.890 | 1.399 | 2.554 | Observed |
#> | mRS6 <= 4 | 1.426 | 1.032 | 1.970 | Observed |
#> | mRS6 <= 5 | 1.065 | 0.744 | 1.525 | Observed |
#> | common OR | 1.657 | 1.274 | 2.155 | Observed |We can also calculate the binary odds ratios and the common odds ratio from elsewhere and supply a data.frame to CORPlot() to make the plot only. The input data.frame must have the following columns:
## use PerforLogReg function to get all binary odds ratios
# We calculate the odds ratio for the group effect, adjusted by sex
# This is done by putting both group and sex in the formula
# and ask for group effect by letting GroupName = "group"
# similarly, if we want the odds ratio of the sex effect, adjusted by group
# we can let GroupName = "sex"
binary_ORs_df <- PerformLogReg(data=df_MR_CLEAN,
formula = mRS6~group+sex,
GroupName = "group",
upper = FALSE)
## use PerformPO to get the common odds ratio
cOR_df <- PerformPO(data=df_MR_CLEAN,
formula = mRS6~group+sex,
GroupName = "group",
upper = FALSE)
## Combine the data.frame
OR_df <- rbind(binary_ORs_df,
cOR_df)
OR_df |>
kable(digits = 3, format = "markdown",
caption = "Binary odds ratios and common odds ratio of the 7-point mRS outcome in the MR CLEAN trial") | Label | OR | lowerCI | upperCI |
|---|---|---|---|
| mRS6 <= 1 | 2.195 | 1.154 | 4.175 |
| mRS6 <= 2 | 2.063 | 1.369 | 3.110 |
| mRS6 <= 3 | 1.878 | 1.312 | 2.690 |
| mRS6 <= 4 | 1.425 | 0.968 | 2.096 |
| mRS6 <= 5 | 1.049 | 0.684 | 1.608 |
| common OR | 1.647 | 1.204 | 2.253 |
Binary odds ratios and common odds ratio of the 7-point mRS outcome in the MR CLEAN trial
## Feed this data.frame to the CORPlot function
res2 <- CORPlot(OR_df = OR_df)
plot(res2)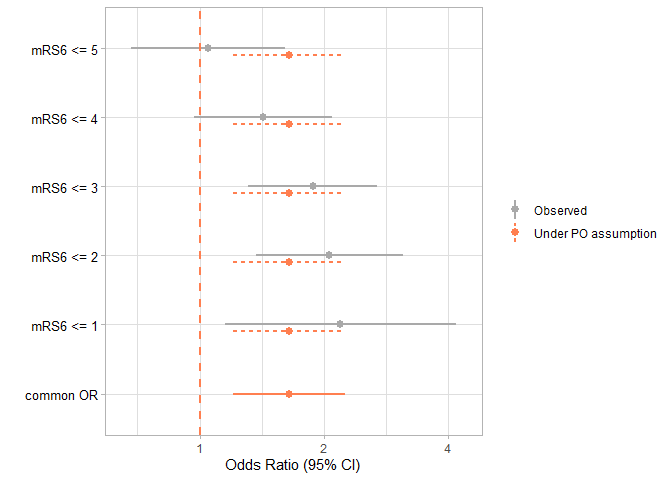
Berkhemer, O. A., Fransen, P. S., Beumer, D., Van Den Berg, L. A., Lingsma, H. F., Yoo, A. J., et al.others. (2015). A randomized trial of intraarterial treatment for acute ischemic stroke. New England Journal of Medicine, 372(1), 11–20.
Long, Y., Wiegers, E. J. A., Jacobs, B. C., Steyerberg, E. W., & Van Zwet, E. W. (2025). Role of the Proportional Odds Assumption for the Analysis of Ordinal Outcomes in Neurologic Trials. Neurology, 105(8), e214146.